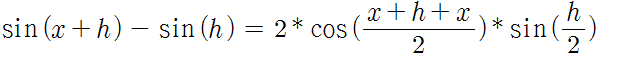더움바다의 일상

오늘은 저번에 이어 React Hook 소개를 이어서 하겠습니다. 첫번째 Hook에 대한 소개는 다음 글에 있습니다. [React] Hook의 이해-1 (useState, useEffect) [React] Hook의 이해-1 (useState, useEffect) 아마 다들 아시겠지만 React18버전 이후로 새로운 공식 문서가 나왔습니다. https://ko.reactjs.org/ (legacy) (reactjs.org는 사라졌는데 ko.reactjs.org는 안 사라졌더라구요.. 개발팀에서 뭔가 실수를 한것 같습 web-story.tistory.com 1. useMemo useMemo는 어떤 값들이 바뀔때만 값을 재계산해주는 hook입니다. const cachedValue = useMemo(calcu..

이번 글에서는 삼각함수 미분 공식 증명을 설명하겠습니다. 미분 공식을 모아둔 글은 다음 링크에 있습니다. [미적분] 미분공식 [미적분] 미분공식 이 글에서는 미분 공식의 기초를 살펴보고, 기본 공식부터 삼각함수의 미분 공식까지 알아보겠습니다. 기본 미분 공식: 미분의 정의에 따라, 함수 f(x)의 도함수를 f'(x) 또는 df/dx로 표기합니다. web-story.tistory.com 사인(sin) 함수 미분 증명 먼저 사인 함수의 미분에 대해 살펴보겠습니다. sin(x)의 미분을 구하기 위해, sin(x + h) - sin(x)를 h에 대해 정리해보겠습니다. sin(x + h) - sin(x) = 2 * cos((x + h + x) / 2) * sin(h / 2) 위의 식을 h로 나누고, h가 0에 근..

이번 글에서는 연쇄 미분 공식의 증명을 살펴보겠습니다. 연쇄 미분 공식의 정의는 다음과 같습니다. 함수 g와 함수 h의 합성함수인 f(x) = g(h(x))가 있을 때, f'(x)는 다음과 같이 표현할 수 있습니다. f'(x) = g'(h(x)) * h'(x) 이제 증명을 해보겠습니다. 먼저, f(x) = g(h(x))의 정의를 사용하여, x와 x + Δx 사이의 f(x)의 변화를 나타내는 f(x + Δx) - f(x)를 구하면 다음과 같습니다. f(x + Δx) - f(x) = g(h(x + Δx)) - g(h(x)) 이제 위 식을 Δx로 나눈 후, Δx가 0에 가까워질 때의 극한을 구하면 다음과 같습니다.. lim (Δx -> 0) [(g(h(x + Δx)) - g(h(x))) / Δx] 이 극한은 ..

이번 글에서는 럼블 소개를 하고자 한다. 스킬들을 먼저 소개를 하자면 다음과 같다.. 패시브 (열 50이상시 기본 스킬들 강화, 열 100시 침묵 & 평타 강화) Q (파이어) W (실드 & 이속증가) E (작살, 마저 감소) R (광역 파이어) 패시브 Q W E R 풀콤보 장점 Q의 광역딜로 인한 빠른 라인 클리어와 강한 초반 맞딜 3,4렙의 절대 강자, 웬만한 챔피언은 거의 다 이긴다. 한타때 궁으로 활약하기 쉽다. 위의 장점들로 인해 스노우볼을 굴리기가 쉽다. 단점 무난하게 반반을 가면 이기기 힘들다. 주력 스킬들의 사거리가 짧기 때문에 후반에 가면 궁셔틀로 전락할수 있다. 1렙때 강한 챔피언들을 상대로 덤볐다간 게임이 하늘로 간다. 럼블은 라인전이 무난한 편이라 상대법을 별로 적을것이 없다. 그렇..

이번 글에서는 통계학에서 자료의 중심과 퍼짐을 나타내는 척도에 대해서 살펴보겠습니다. 자료의 중심 척도에는 평균, 중앙값, 최빈값이 있습니다. 평균 (Mean) 평균은 모든 데이터의 합을 데이터의 개수로 나눈 값으로, 가장 많이 사용하는 척도입니다. 공식: (Σx_i) / n 여기서 x_i는 각 데이터 값이며, n은 데이터의 개수입니다. 중앙값 (Median) 중앙값은 데이터를 크기 순으로 정렬했을 때 가장 가운데 위치하는 값입니다. 데이터의 개수가 짝수일 경우, 가운데 두 값의 평균이 중앙값이 됩니다. 중앙값은 이상치에 영향을 받지 않아, 평균보다 데이터의 중심을 더 잘 나타낼 때도 있습니다. 최빈값 (Mode) 최빈값은 데이터에서 가장 자주 등장하는 값입니다. 범주형 데이터의 경우, 최빈값은 가장 많..