이번 글에서는 통계학에서 자료의 중심과 퍼짐을 나타내는 척도에 대해서 살펴보겠습니다.
자료의 중심 척도에는 평균, 중앙값, 최빈값이 있습니다.
평균 (Mean)
- 평균은 모든 데이터의 합을 데이터의 개수로 나눈 값으로, 가장 많이 사용하는 척도입니다.
- 공식: (Σx_i) / n
- 여기서 x_i는 각 데이터 값이며, n은 데이터의 개수입니다.

중앙값 (Median)
- 중앙값은 데이터를 크기 순으로 정렬했을 때 가장 가운데 위치하는 값입니다.
- 데이터의 개수가 짝수일 경우, 가운데 두 값의 평균이 중앙값이 됩니다.
- 중앙값은 이상치에 영향을 받지 않아, 평균보다 데이터의 중심을 더 잘 나타낼 때도 있습니다.
최빈값 (Mode)
- 최빈값은 데이터에서 가장 자주 등장하는 값입니다.
- 범주형 데이터의 경우, 최빈값은 가장 많은 빈도를 가진 범주를 나타냅니다.
- 연속형 데이터에서는 최빈값을 구하기 어렵기 때문에, 데이터를 구간으로 나누어 각 구간의 빈도를 분석하는 방법을 사용할 수 있습니다.
자료의 퍼짐 척도에는 범위, 사분위수 범위, 분산, 표준편차가 있습니다.
범위 (Range)
- 범위는 데이터에서 최대값과 최소값의 차이를 나타냅니다.
- 범위는 계산하기 쉽지만, 이상값(극단적인 값)에 민감하며 전체 데이터의 분산을 정확하게 반영하지 못하는 단점이 있습니다.
사분위수 범위 (Interquartile Range, IQR)
- 사분위수 범위는 데이터의 하위 25%(제1사분위수, Q1)와 상위 25%(제3사분위수, Q3)의 차이를 나타냅니다.
- IQR은 이상치에 영향을 받지 않으므로, 범위보다 데이터의 퍼짐을 더 잘 나타낼 수 있습니다.
분산 (Varience)
- 분산은 각 데이터 값과 평균 사이의 차이를 제곱한 값의 평균입니다.
- 분산은 데이터의 퍼짐 정도를 잘 나타냅니다.
- 공식: Σ(x_i - mean)^2 / n
- 여기서 x_i는 각 데이터 값이며, mean은 평균, n은 데이터의 개수입니다.
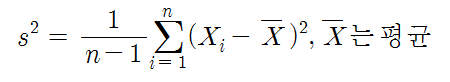
표준편차 (Standard Deviation)
- 표준편차는 분산의 제곱근으로, 분산과 마찬가지로 데이터의 퍼짐 정도를 잘 나타냅니다.
- 공식: √(Σ(x_i - mean)^2 / n)

'Study > 통계학' 카테고리의 다른 글
| [통계학] 결합사상과 조건부 확률 (0) | 2023.05.15 |
|---|---|
| [통계학] 확률 (2) | 2023.05.13 |
| [통계학] 통계학의 이해 (0) | 2023.04.18 |