이번 글에서는 연쇄 미분 공식의 증명을 살펴보겠습니다.
연쇄 미분 공식의 정의는 다음과 같습니다.
함수 g와 함수 h의 합성함수인 f(x) = g(h(x))가 있을 때, f'(x)는 다음과 같이 표현할 수 있습니다.
f'(x) = g'(h(x)) * h'(x)

이제 증명을 해보겠습니다.
먼저, f(x) = g(h(x))의 정의를 사용하여, x와 x + Δx 사이의 f(x)의 변화를 나타내는 f(x + Δx) - f(x)를 구하면 다음과 같습니다.
f(x + Δx) - f(x) = g(h(x + Δx)) - g(h(x))
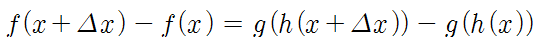
이제 위 식을 Δx로 나눈 후, Δx가 0에 가까워질 때의 극한을 구하면 다음과 같습니다..
lim (Δx -> 0) [(g(h(x + Δx)) - g(h(x))) / Δx]

이 극한은 f'(x)에 해당합니다. 그러나 이 형태로는 바로 계산하기 어렵습니다.바로 계산하기 어렵기에 치환을 이용해야 합니다. 치환을 이용해서 y = h(x)로 두면 다음과 같습니다.
y + Δy = h(x + Δx)
Δy = h(x + Δx) - h(x)

이를 이용하면 위 극한 식을 다음과 같이 바꿀 수 있습니다.
lim (Δx -> 0) [(g(y + Δy) - g(y)) / Δx]

이제 극한의 분자와 분모를 Δy로 나누고, Δx가 0에 가까워질 때 Δy도 0에 가까워진다는 점을 이용하여 다음과 같이 바꿉니다.
lim (Δy -> 0) [(g(y + Δy) - g(y)) / Δy] * lim (Δx -> 0) [Δy / Δx]

이제 각 극한을 계산할 수 있습니다.
lim (Δy -> 0) [(g(y + Δy) - g(y)) / Δy] = g'(y)
lim (Δx -> 0) [Δy / Δx] = h'(x)

위 두 극한을 곱하면 최종적으로 다음 결과를 얻게 됩니다.
f'(x) = g'(y) * h'(x)

여기서 y = h(x)이므로, f'(x)를 다음과 같이 표현할 수 있습니다.
f'(x) = g'(h(x)) * h'(x)
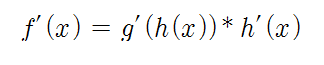
전체 순서
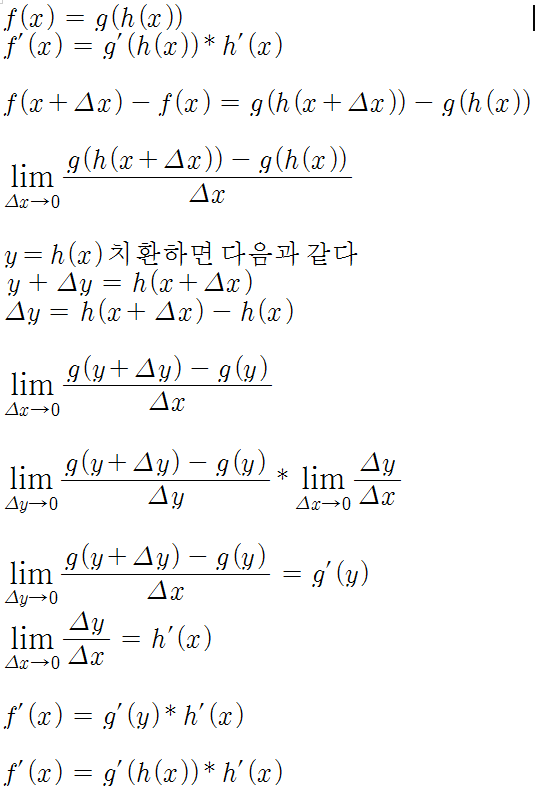
오늘은 이것으로 연쇄 미분공식의 증명을 알아보았습니다. 감사합니다

'Study > 수학' 카테고리의 다른 글
| [미적분] 삼각함수 미분 공식의 증명 (0) | 2023.04.25 |
|---|---|
| [미적분] 합, 차, 곱, 분수 미분 공식의 증명 (2) | 2023.04.18 |
| [미적분] 기본 미분 공식의 증명 (0) | 2023.04.17 |