오늘은 기본적인 미분공식의 증명에 대해 설명하겠습니다.
대표적인 미분 공식들은 다음 글에 있습니다.
[미적분] 미분공식
이 글에서는 미분 공식의 기초를 살펴보고, 기본 공식부터 삼각함수의 미분 공식까지 알아보겠습니다. 기본 미분 공식: 미분의 정의에 따라, 함수 f(x)의 도함수를 f'(x) 또는 df/dx로 표기합니다.
web-story.tistory.com
미분의 정의는 다음과 같습니다
f'(x) = lim(h->0) [(f(x+h)-f(x))/h]
여기서 f'(x)는 함수 f의 도함수를 의미합니다. 또한 이 정의를 통해 기본 미분공식을 증명할 수 있습니다.

1. 상수함수 미분 증명:
- f(x) = c, c는 상수
- f'(x) = lim(h->0) [(c-c)/h] = 0

2. 거듭제곱 함수 미분 증명:
- f'(x) = x^n
- f'(x) = lim(h->0) [((x+h)^n - x^n)/h]

증명:
이항정리를 이용하여 (x+h)^n을 전개합니다.
- (x+y)^n = Σ(C(n, k) * x^(n-k) * y^k) (k=0부터 n까지)
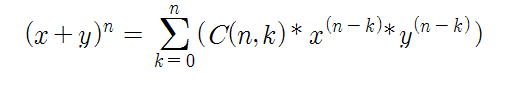
여기서 C(n, k)는 조합(combination)으로, n! / (k!(n-k)!)로 정의됩니다.
이를 이용하여 (x+h)^n을 전개하면 다음과 같습니다.
- (x+h)^n = x^n + nC1 * x^(n-1) * h + nC2 * x^(n-2) * h^2 + ... + nCn * h^n

이제 이를 f'(x) = lim(h->0) [((x+h)^n - x^n)/h]에 대입합니다.
- f'(x) = lim(h->0) [(x^n + nC1 * x^(n-1) * h + nC2 * x^(n-2) * h^2 + ... + nCn * h^n - x^n)/h]
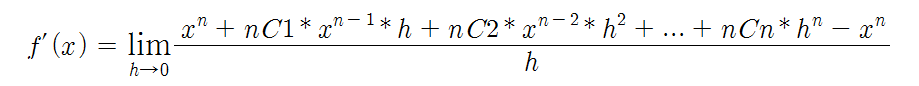
식을 간략화하면 다음과 같습니다.
- f'(x) = lim(h->0) [nC1 * x^(n-1) + nC2 * x^(n-2) * h + ... + nCn * h^(n-1)]
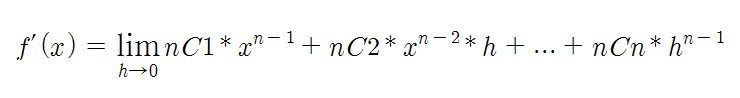
h가 0으로 수렴하므로, h의 거듭제곱 항들은 모두 0으로 수렴하게 됩니다. 따라서 f'(x)는 다음과 같이 간단하게 표현됩니다.
- f'(x) = nC1 * x^(n-1)
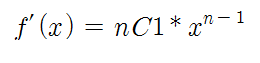
여기서 nC1은 n! / (1!(n-1)!)이므로, nC1 = n입니다. 결과적으로 다음과 같은 미분 공식이 얻어집니다.
- f'(x) = nx^(n-1)
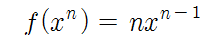
'Study > 수학' 카테고리의 다른 글
| [미적분] 합, 차, 곱, 분수 미분 공식의 증명 (2) | 2023.04.18 |
|---|---|
| [미적분] 미분공식 (0) | 2023.04.16 |
| [미적분] 미분계수와 도함수 (0) | 2023.04.15 |