이 글에서는 미분 공식의 기초를 살펴보고, 기본 공식부터 삼각함수의 미분 공식까지 알아보겠습니다.
기본 미분 공식:
- 미분의 정의에 따라, 함수 f(x)의 도함수를 f'(x) 또는 df/dx로 표기합니다. 다음은 몇 가지 기본 미분 공식입니다.
- 상수 미분: c'(x) = 0 (c는 상수)

- 일차 함수 미분: (x^n)' = nx^(n-1) (n은 자연수)합, 차, 곱, 분수의 미분 공식:

2. 두 함수 f(x)와 g(x)에 대한 합, 차, 곱, 분수의 미분 공식은 다음과 같습니다.
- 합의 미분: (f(x) + g(x))' = f'(x) + g'(x)

- 차의 미분: (f(x) - g(x))' = f'(x) - g'(x)
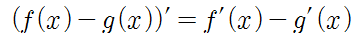
- 곱의 미분 (곱셈 법칙): (f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x)
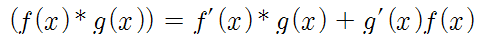
- 분수의 미분 (분수 법칙): (f(x) / g(x))' = (f'(x) * g(x) - f(x) * g'(x)) / g(x)^2
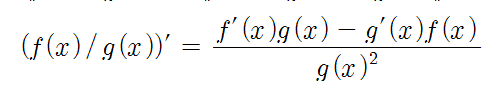
연쇄 미분 공식 (Chain Rule):
- 복합 함수의 미분은 연쇄 법칙을 사용하여 계산할 수 있습니다. 연쇄 법칙은 다음과 같습니다.
- (f(g(x)))' = f'(g(x)) * g'(x)

자연로그 미분 공식:
- e^x 미분: (e^x)' = e^x
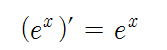
삼각함수 미분 공식:
- sin(x) 미분: (sin(x))' = cos(x)

- cos(x) 미분: (cos(x))' = -sin(x)

- tan(x) 미분: (tan(x))' = sec^2(x)
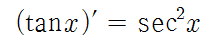
- cot(x) 미분: (cot(x))' = -csc^2(x)
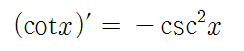
- sec(x) 미분: (sec(x))' = sec(x) * tan(x)

- csc(x) 미분: (csc(x))' = -csc(x) * cot(x)
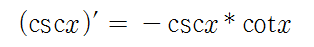
'Study > 수학' 카테고리의 다른 글
| [미적분] 합, 차, 곱, 분수 미분 공식의 증명 (2) | 2023.04.18 |
|---|---|
| [미적분] 기본 미분 공식의 증명 (0) | 2023.04.17 |
| [미적분] 미분계수와 도함수 (0) | 2023.04.15 |