이번 글에서는 적분에 대해 다뤄보겠습니다
적분이란 뭘까요?
쉽게 생각하자면 어떤 도형의 넓이를 구하는 것입니다.
어렸을때는 사각형의 넓이를 구하는것을 가로 x 세로라고 배웠었죠.
적분의 개념도 비슷합니다.

가로 x 세로는 아니지만 가로 x 세로에요.

무슨 말이냐면 이렇게 하나의 도형을 여러개의 작은 사각형으로 분할합니다.
물론 처음에는 빈 공간이 발생하겠죠.
하지만 아래 그림에서 나오다싶이 처음에는 노란색 사각형처럼 큼지막하게 분할하다
두번째에는 초록색 사각형처럼 좀더 잘게 분할하는 모습을 보실수 있습니다.
이와 같이 점점더 잘게 분할하게 되면 도형의 넓이를 사각형의 넓이를 구하는 방식과 같이 구할수 있습니다.
바로 1번 사각형의 넓이 + 2번 사각형의 넓이 + 3번 사각형의 넓이 ... + 마지막 사각형의 넓이처럼 말이죠.

그렇다면 기호로는 어떻게 표기할까요?
바로 다음과 같이 표기하고 인테그랄이라고 읽습니다.

그러면 이런 적분을 도대체 어디에 사용할까요?
더 많은 예시가 있겠지만 이 세가지 분야에서의 사용처를 알려드리겠습니다.
- 물리학
- 경제학
- 통계학
물리학

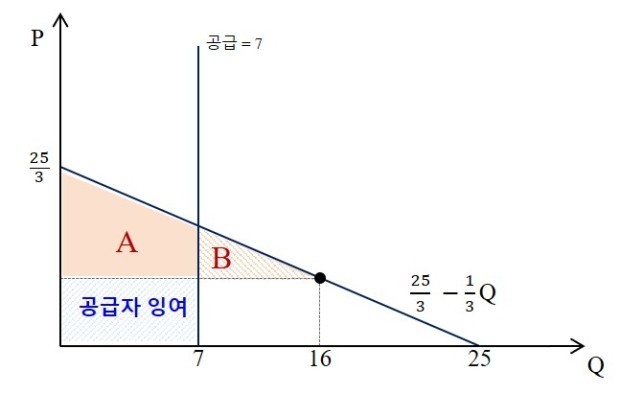
경제학
통계학

오늘은 간단하게 적분에 대해 소개해 드렸고 다음 글에서는 증명을 해보도록 하겠습니다.
긴 글 봐주셔서 감사합니다.

'Study > 수학' 카테고리의 다른 글
| [미적분] 적분공식 (0) | 2024.05.23 |
|---|---|
| [선형대수] 벡터의 연산(덧셈, 뺄셈) (0) | 2023.12.19 |
| [선형대수] 스칼라와 벡터 (0) | 2023.12.14 |