이 글에서는 적분의 기본 공식을 간단히 알아보겠습니다.
우선 적분은 크게 정적분과 부정적분으로 나눌수 있습니다.
부정적분은 미분의 역연산입니다. 기호 ∫f(x)dx로 표현됩니다.
예를 들어, ∫x²dx는 x³/3 + C입니다. 여기서 C는 적분 상수입니다.
부정적분의 기본 공식
- 기본 적분 공식: ∫xⁿdx = (xⁿ⁺¹)/(n+1) + C (단, n ≠ -1)

- 상수의 적분: ∫a dx = ax + C
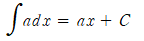
- 지수 함수의 적분: ∫eˣdx = eˣ + C

삼각함수 적분 공식
- sin 적분: ∫sin(x)dx = -cos(x) + C

- cos 적분: ∫cos(x)dx = sin(x) + C
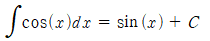
- sec 적분: ∫sec²(x)dx = tan(x) + C
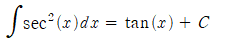
정적분의 기본 공식
정적분은 구간 [a, b]에서 함수 f(x)의 넓이를 구하는 과정입니다.
기호 ∫[a, b] f(x)dx로 표현됩니다. 정적분으로는 실제 면적을 구할 수 있습니다.
공식: ∫[a, b] f(x)dx = F(b) - F(a)

'Study > 수학' 카테고리의 다른 글
| [미적분] 정적분과 증명 (0) | 2024.07.10 |
|---|---|
| [미적분] 적분의 개념 (0) | 2024.01.07 |
| [선형대수] 벡터의 연산(덧셈, 뺄셈) (0) | 2023.12.19 |