이번 글에서는 정적분의 성질에 대해서 다뤄보겠습니다.
정적분의 성질로는 5가지 정도가 있습니다.
- 적분 순서
- 상수배
- 합과 차
- 가법성
- 최대-최소 부등식
적분 순서 (성질)
적분 순서 성질은 말 그대로 순서에 관한 성질입니다.

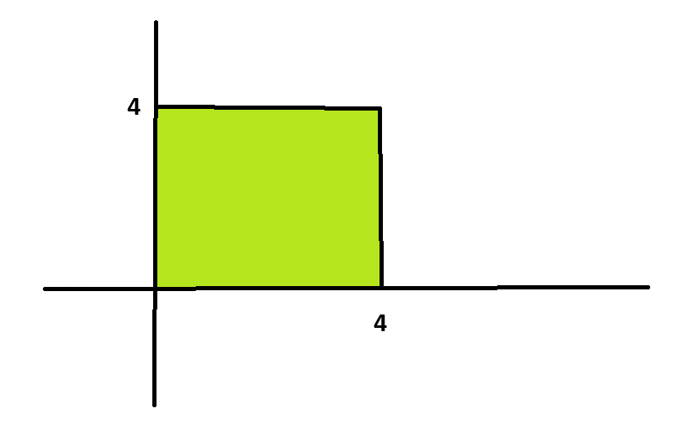
[a,b]구간의 면적과 [b,a]구간의 면적에 -1을 곱해준 면적과 동일하다는 성질입니다.
사각형의 넓이를 구할때 (4-0) x 4와 (0-4) x 4 x (-1)과 동일하다는 것과 같습니다.
상수배 (성질)
상수배 성질은 다음과 같습니다.

적분은 결국에 리먼합을 이용해서 구하게 됩니다.
리먼합에서는 시그마를 사용합니다.
시그마의 성질중에 시그마 안의 함수에 상수배를 밖으로 꺼낼수가 있는데 해당 원리로 적분에서도 상수배를 꺼낼수 있다고 생각해주시면 될것 같습니다.
합과 차 (성질)
합과 차 성질은 단순하게 덧셈 뺄셈입니다.

젠가 탑을 쌓을때 박스안에 집어넣고 모양을 만들어서 꺼내나 젠가를 일일이 꺼내서 만드나 동일한것과 같다고 생각해주시면 될것 같습니다.
가법성 (성질)
가법성의 성질에서는 조건이 좀 필요한데 선이 이어져야 됩니다.

(그림이 좀 안맞기는 한데 넘어가주시면 감사하겠습니다...)
위 이미지의 직사각형에서는
4 x 4 + 2 x 4 = 6 x 4 이라는 식이 성립하게 됩니다.
y선이 4로 같기 때문이죠.

하지만 바로 아래의 직사각형에서는
4 x 4 + 2 x 4 = 6 x 4 이라는 식이 성립하지 않습니다.
연두색 직사각형에서는 y가 4고 초록색 직사각형에서는 y가 6이기 때문이죠.

가법성의 원리도 이와 비슷합니다
f(x)가 이어질때 성립한다고 생각해주시면 될것 같습니다.
최대 - 최소 부등식 (성질)
함수 f가 [a,b] 구간에서 최솟값과 최댓값을 가졌을때 정적분의 값은 항상 그안에 들어간다는 성질입니다.


위 이미지에서 노란색 + 연두색으로 색칠된 넓이는 y를 MaxF로 계산하고 x를 b - a의 값으로 계산한 직사각형보다는 항상 작을것이고 연두색으로 색칠된 부분(y를 minf로 계산)보다는 항상 넓겠죠.
최대 - 최소 부등식의 성질은 이와 같습니다.
오늘은 정적분의 성질에 대해 간단히 알아보았습니다.
오늘도 긴글 봐주셔서 감사합니다.

'Study > 수학' 카테고리의 다른 글
| [선형대수] 벡터와 기본 공식 (0) | 2024.08.25 |
|---|---|
| [미적분] 정적분과 증명 (0) | 2024.07.10 |
| [미적분] 적분공식 (0) | 2024.05.23 |