이 글에서는 정적분의 기본 공식에 대해 간단히 증명해보겠습니다.
우선 정적분이란 함수 f(x)가 주어진 구간 [a,b]에서 연속일때, a에서 b까지의 면적을 계산하는 방법입니다.
공식은 다음과 같습니다.

해당 식은 f(x)가 [a,b]에서 정적분된 값을 의미합니다.
즉 f(x)와 x축사이의 면적을 의미합니다.

그래서 정적분의 핵심 공식은 다음과 같습니다.
이렇게 보면 어렵긴 한데 사각형 넓이 구하는 공식이랑 비슷하다고 생각해주시면 될것 같아요.

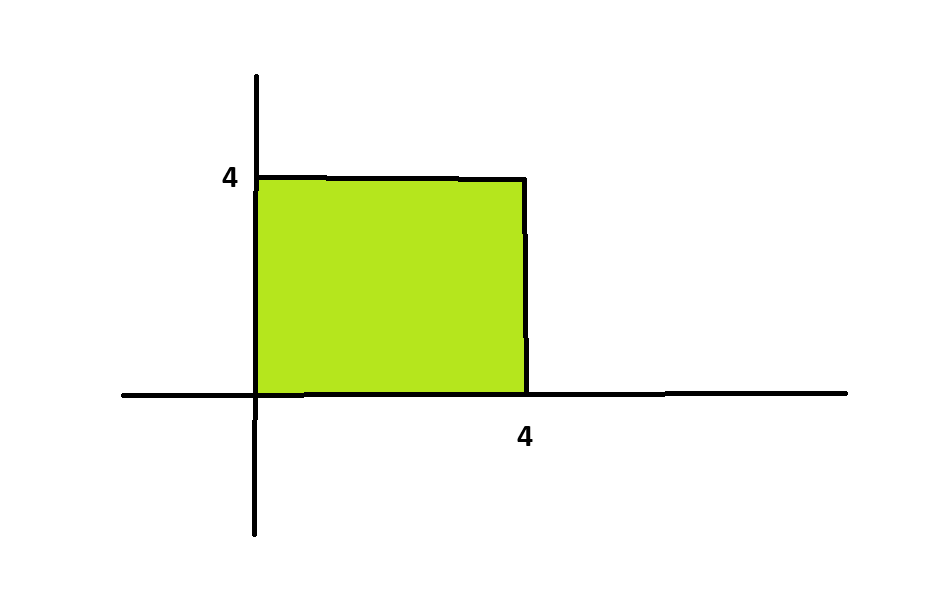
사각형 넓이 (4 - 0) * (4 - 0) = 16
정적분 공식도 비슷하게 b-a에 f(x)를 씌우기만 하면 됩니다.
다만 여기서 F는 의 부정적분 또는 원시 함수입니다. 즉, F′(x)=f(x)를 만족하는 함수입니다.
(쉽게 미분을 뒤집으면 됩니다)

이제 증명을 해보겠습니다.
- 기본 가정
- 먼저 함수 가 [a,b]구간에서 연속이고, F가 f의 부정적분이라고 가정해봅시다. 즉, F′(x)=f(x)입니다.
- 부분 구간
- [a,b] 구간을 n개의 작은 소구간으로 다시 나눕니다. 각 구간의 폭은 z = (b-a)/n입니다.
- 각 작은 구간의 오른쪽 끝점을 x_i라 하며 x_iㄴ = a + i * z입니다.
- (여기서 i는 0부터 n까지의 정수입니다)
- 함수 f의 각 작은 구간에서의 값을 f(x_i)로 근사시킵니다.
- 리먼 합
- 함수 f의 정적분은 작은 구간들에서의 함수 값을 더함으로써 근사시킬수 있습니다.
- 이를 리먼합이라고 합니다.
- (x_{i}^{*}는 각 구간 내의 임의의 점입니다)

- 리먼 합과 부정적분의 관계
- 리먼 합 S_n을 부정적분 F로 표현하면 다음과 같습니다

- 정리
- 위 식을 정리해보자면 다음과 같습니다

- 결론
- 따라서 리먼 합 S_n이 무한대로 갈때 정적분의 값으로 수렴합니다.

간단한 예제를 한번 사용해보겠습니다.
문제: f(x) = x^2일 때 [1,5] 구간에서의 정적분을 계산하시오.
1. 부정적분을 구합니다.

2. 정적분 공식을 사용합니다.
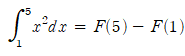
3. 부정적분의 값을 대입해서 계산합니다.

4. 정답: 124/3
오늘은 정적분의 공식과 증명에 대해 간단히 알아보았습니다.
다음 글에서는 정적분의 성질에 대해 간단히 다뤄보고자 합니다.
오늘도 긴 글 봐주셔서 감사합니다.

'Study > 수학' 카테고리의 다른 글
| [미적분] 정적분의 성질 (2) | 2024.07.12 |
|---|---|
| [미적분] 적분공식 (0) | 2024.05.23 |
| [미적분] 적분의 개념 (0) | 2024.01.07 |