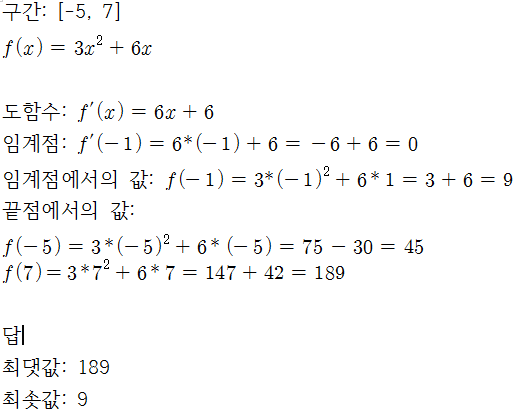더움바다의 일상

오늘은 함수의 극값을 구하는 방법에 대해 알아보겠습니다. 1. 극값이란? 지난 포스트에서도 설명드렸다싶이 주어진 함수의 특정 지점에서 그 주변의 다른 값들보다 큰 값 혹은 작은 값을 갖는 곳을 의미합니다. 더욱 자세한 설명은 포스트를 봐주시면 감사하겠습니다. [미적분] 함수의 극값 [미적분] 함수의 극값 오늘은 함수의 극값에 대해 알아보겠습니다. 함수의 극값은 절대 극값(최댓값, 최솟값)과 국소 극값(극댓값, 극솟값)으로 구분할수 있습니다. 최댓값과 최솟값 (절대 극값) 함수의 최댓값이란 함 web-story.tistory.com 2. 극값을 찾는 방법 극값을 찾는 방법에는 두가지 방법이 있지만 오늘은 임계점을 찾아 절대 극값을 구하는 방법에 대해서만 알아보겠습니다. 임계점을 찾는 방법 2계 도함수를 활..

이번 글에서는 삼각함수 미분 공식 증명을 설명하겠습니다. 미분 공식을 모아둔 글은 다음 링크에 있습니다. [미적분] 미분공식 [미적분] 미분공식 이 글에서는 미분 공식의 기초를 살펴보고, 기본 공식부터 삼각함수의 미분 공식까지 알아보겠습니다. 기본 미분 공식: 미분의 정의에 따라, 함수 f(x)의 도함수를 f'(x) 또는 df/dx로 표기합니다. web-story.tistory.com 사인(sin) 함수 미분 증명 먼저 사인 함수의 미분에 대해 살펴보겠습니다. sin(x)의 미분을 구하기 위해, sin(x + h) - sin(x)를 h에 대해 정리해보겠습니다. sin(x + h) - sin(x) = 2 * cos((x + h + x) / 2) * sin(h / 2) 위의 식을 h로 나누고, h가 0에 근..

이번 글에서는 연쇄 미분 공식의 증명을 살펴보겠습니다. 연쇄 미분 공식의 정의는 다음과 같습니다. 함수 g와 함수 h의 합성함수인 f(x) = g(h(x))가 있을 때, f'(x)는 다음과 같이 표현할 수 있습니다. f'(x) = g'(h(x)) * h'(x) 이제 증명을 해보겠습니다. 먼저, f(x) = g(h(x))의 정의를 사용하여, x와 x + Δx 사이의 f(x)의 변화를 나타내는 f(x + Δx) - f(x)를 구하면 다음과 같습니다. f(x + Δx) - f(x) = g(h(x + Δx)) - g(h(x)) 이제 위 식을 Δx로 나눈 후, Δx가 0에 가까워질 때의 극한을 구하면 다음과 같습니다.. lim (Δx -> 0) [(g(h(x + Δx)) - g(h(x))) / Δx] 이 극한은 ..

오늘은 기본적인 미분공식의 증명에 대해 설명하겠습니다. 대표적인 미분 공식들은 다음 글에 있습니다. [미적분] 미분공식 [미적분] 미분공식 이 글에서는 미분 공식의 기초를 살펴보고, 기본 공식부터 삼각함수의 미분 공식까지 알아보겠습니다. 기본 미분 공식: 미분의 정의에 따라, 함수 f(x)의 도함수를 f'(x) 또는 df/dx로 표기합니다. web-story.tistory.com 합의 미분 공식 합의 미분 공식은 두 함수의 합의 미분이 각 함수의 미분의 합과 같다는 것을 나타냅니다. (g(x) + h(x))' = g'(x) + h'(x) 증명: f'(x) = lim(h->0) [(g(x+h) + h(x+h)) - (g(x) + h(x))]/h = lim(h->0) [(g(x+h) - g(x))/h + (..

오늘은 기본적인 미분공식의 증명에 대해 설명하겠습니다. 대표적인 미분 공식들은 다음 글에 있습니다. [미적분] 미분공식 [미적분] 미분공식 이 글에서는 미분 공식의 기초를 살펴보고, 기본 공식부터 삼각함수의 미분 공식까지 알아보겠습니다. 기본 미분 공식: 미분의 정의에 따라, 함수 f(x)의 도함수를 f'(x) 또는 df/dx로 표기합니다. web-story.tistory.com 미분의 정의는 다음과 같습니다 f'(x) = lim(h->0) [(f(x+h)-f(x))/h] 여기서 f'(x)는 함수 f의 도함수를 의미합니다. 또한 이 정의를 통해 기본 미분공식을 증명할 수 있습니다. 1. 상수함수 미분 증명: f(x) = c, c는 상수 f'(x) = lim(h->0) [(c-c)/h] = 0 2. 거듭제..