안녕하세요. 오늘은 확률의 공리와 몇가지 명제에 대해 다루어보겠습니다.
확률의 공리란 수학에서 증명을 하지 않기로 약속한, 즉 당연한 것으로 가정하는 명제인데요.
크게 3가지가 있습니다.
- 공리 1
- 모든 확률은 0보다 크고 1보다 작다.

- 공리 2
- 표본공간 S에서의 확률은 1이다.
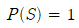
- 공리 3
- 상호 배반인 임의의 사건 E_1, E_2... 등에 대해 다음식이 성립한다.

확률의 공리를 바탕으로 몇가지 명제를 도출할수 있습니다.
- A의 여사건의 확률은 1 - A의 확률과 같습니다.

- 두 사건 A와 B에 대해 A U B의 확률은 A + B - A n B의 확률과 같습니다.

- 두 사건 A와 B가 일어날 확률은 다음과 같습니다.

- 사건 B가 일어났다는 전제 하에 A의 확률은 다음과 같습니다.

- B_1, B_2...가 전부 상호배반이고 합집합이 표본공간 S일때 A의 확률은 다음과 같습니다.

- 조건부 정리를 이용하여 B가 일어났다는 전제 하에 A의 확률을 다음과 같은 공식으로 구할수 있습니다 (베이즈 정리)

오늘은 확률의 공리와 명제에 대해 간단히 알아보았습니다.
오늘도 긴글 봐주셔서 감사합니다.

'Study > 통계학' 카테고리의 다른 글
| [확률] 표본공간과 사건 (0) | 2024.08.12 |
|---|---|
| [확률] 다항계수와 증명 (2) | 2024.07.21 |
| [확률] 이항정리와 증명 (2) | 2024.07.17 |